こんにちは。株式会社SHIFT、自動化エンジニアの水谷です。

SHIFTではテスト設計の段階でPairwise（All-pairとも言われます）の考え方を取り入れることがあります。テストをしていると、全網羅でカバー率100％のテストを行うことが時間的に（工数的に）難しい場面がありますよね？　そんな時にはPairwiseを使うことで、テストケース数を大幅に減らしつつバグ発見率は高い状態を保つことができるとされています。

Pairwiseはソフトウェアテスターにとっては知っておくべき考え方の１つ言われるほど重要なものなのですが、今回はこれを実現する代表的なツールの1つであるPICTについて、筆者が最近ふと思い出したことや、そのアルゴリズムについて調べたことなどを書いてみたいと思います。

Pairwiseについて

Pairwiseについては、ネットに多くの情報があるので、それらを見ていただいたほうが早いかと思いますが、基本的には以下のリサーチ結果をもとにしています。

例えば10個パラメーター（因子）があったとしても、そのすべてが特定の値だった場合のみ不具合が発生するような問題はほとんどなく、パラメーターのうちの2個あるいは3個が特定の組み合わせの場合に発生しているというのです。

そこで、Pairwiseでは、たくさんあるパラメーターのうちのどの2つ（あるいは３つ）のパラメーターについては、それぞれの取りうる値（水準）の組み合わせを網羅するけど、それ以外の組み合わせについては網羅しない、とすることでテストケースを減らそうというのです。

今のPICTは第2世代

Pairwiseの考え方を使ってテストケースの組み合わせを生成してくれるツールの１つに、Microsoftで作られた「PICT」があります。Pairwiseと言えばPICTというほど有名なツールなのですが、私がこのツールに出会ったのは、確か2003年頃だったかと思います。調べてみると、MicrosoftでPICTが使われ始めたのは2000年とされているので、そこから20年が経っても今なお現役で使われている手法とツールということになります。

私がSHIFTに入社して、SHIFTがPICTを使っていると知った時、PICTに関するあるエピソードを思い出しました。PICTの原作者はDavid Erbという名のMicrosoftの開発者だったのですが、当時彼はこのツールがこれほど広く、長く使われるとは思っていなかったのか、PICTのソースコードはソースコード管理ツールにアップロードするどころか、他のエンジニアに共有することすらせず、彼のPCにだけ保存していたそうです。

そして彼が退社すると同時に、ソースコードがどこにもない、ロスト状態になってしまうのです。そんな状況とは裏腹に、（このツールはとても有用だったため）PICTのバイナリファイルだけが社内のテストエンジニアの間でどんどん広まっていったそうです。つまり、どうやって動いているかはわからないけどテスターにとっては無くてはならない便利なツールになっていったというわけです。

私の記憶が正しければ、このオリジナルのPICTには最新のPICTに比べてずっとシンプルで、今のPICTが持っているような便利な機能は作りこまれていませんでした。ソースコードがないので新しい機能を追加したくてもそれができず、ありのままのPICTを使う以外選択肢がない状態が続いていたのですが、その3年後、PICTはMicrosoftの基礎研究機関であるMicrosoft Researchによって作り直されたようです。

新しいPICTがオリジナルのPICTのバイナリを解析して作られたのか、それとも1から作ったのかはわかりませんが、新しいPICTにはオリジナルのPICTにはなかった機能がたくさん盛り込まれ、そのソースコードはGitで公開されています。つまり、ソースコードがなかった時代から一転して、だれでもソースコードを読むことができ、改良に貢献することもできるのです。さらに、PICTの内部構造や拡張機能について記した論文も発表されているので、PICTについて知りたい場合はこれを読むこともできます。

PICTの論文からわかること

実際この論文「Pairwise Testing in the Real World: Practical Extensions to Test-Case Scenarios」を読んでみたのですが、そこから２つ興味深いことを知ることができました。１つは、この新しいPICTに追加されている機能がとても豊富なことです。列挙してみるとこのようなものです。

・Mixed-Strength Generation
・Creating a Parameter Hierarchy
・Excluding Unwanted Combinations
・Seeding
・Testing with Negative Values
・Assigning Weights to Values

PICTをさらに便利に使うためには、これらの機能についても知っておきたいところですので、別の機会に1つずつ解説してみたいと思います。

2つ目は、PICTのアルゴリズムが解説されていることです。
各2パラメーター（2因子）を全網羅していくこと自体はさほど難しい話ではなく、因子数が少なければプログラムを使わなくてもこれを満たすテストケース群が作れます。しかし、いざプログラムあるいはスクリプトを書いてこれを汎用的に実装しようと思うと、なかなか簡単には書けません（少なくとも私のレベルでは……）。

と言うのも、単に各2パラメーターを全網羅するテストケースを作るだけならできても、それを“できるだけ少ないテストケース数で実現する”、という点がポイントで、これがとても難しいのです。また、3因子間の網羅もできるようにしようとするとこれがまた面倒だし、ましてやこれを一般化してN因子間網羅を可能にしようとすると、相当考えないといけなくなります。

さらに、因子や水準が多いと当然テストケース作成にかかる時間は当然長くなるのですが、これが指数関数的に長くなってしまっては使えないツールになってしまいますので、いわゆる多項式時間で処理が終わるロジックを考えて実装する必要があります。

このように実装方法を少し考えるといろいろ難しい点が見えてくるPairwiseですが、ではこのPICTはどのようなアルゴリズムを使って実装されているのでしょうか？

貪欲法という名前で笑ってしまいそうになるアルゴリズム

論文を読んでいくと、PICTで使っているアルゴリズムは”Greedy Heuristic”だと書かれています。日本では“グリーディー算法”、あるいは直訳の“貪欲法”の名で知られているものです。また、後ろの“Heuristic”は、それが発見的手法であることを表しています。つまり、必ず正しい答えが導けるわけではないが、短い時間で正解に近い答えが出せるアルゴリズム、ということになります。

この貪欲法というアルゴリズムは、アルゴリズムを勉強された方はご存じかもしれませんが、そうでない方にとってはあまり耳にしたことのないものではないかと思います。かくいう自分もPICTを調べるまでは知りませんでした。しかし、その内容は難しいものではなく、ざっくり書いてしまうと、全体のことは考えずその場その場で最適な選択をしていく（局所的最適化）ことで、“もしかしたらベストではないかもしれないけれど十分に使える良い結果を短い処理時間で得よう”、というものです。

この貪欲法を使って、PICTは以下のような処理をすると記されています。

因子の数は2つではなく任意な値とした一般化した状態で書かれており、（後日書く予定の）seedingやexcludingの概念も入っているのでやや理解しにくいかもしれません。

そこでズバッとシンプルにして、因子数が３つで2因子網羅の簡単な例を元にこれを読み砕いてみたいと思います。

アルゴリズムを追ってシンプルな2因子間網羅をやってみる

では、実際に下のようなとても簡単な例で試してみましょう。

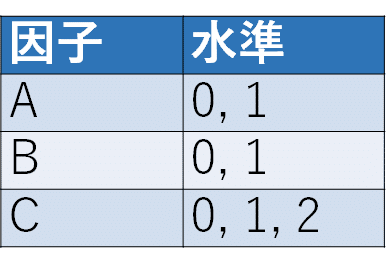
因子はABCの3つがあり、水準数は順に２、２、３としていますので、全網羅すると2×2×３＝12通りになります。

まず準備段階として、各2因子の網羅表を作ります（下の表）。実際PICTもこの表を作ることから始まります。

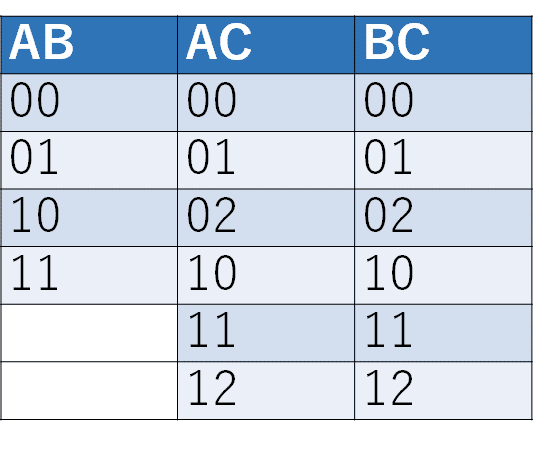
ここで、この表の各マスのことをスロットと呼ぶことにします（論文ではslotと表記されています）。そして、この表から“ある法則”に従ってスロットを選んでテストケースを作っていきます。どんどん使っていないスロットを使っていき、すべてのスロットが使われた時点で作成完成、テストケースの生成が完了です。

さて、ここからの説明をわかりやすくするため、未使用のスロットは白色で、使用済みのスロットは緑に色を付けることにします（直近使ったスロットは濃い緑、すでに使われていたスロットは薄い緑です）。なお、PICTではその時点で選択できるスロットが複数ある場合は、その中からランダムに１つ選択するのですが、ここではわかりやすくするために、ランダムではなく、上の表内でできるだけ左（BC列よりAC行、AC行よりAB行）で、できるだけ上のスロットを選ぶことにします。

さてPICTの論文によると、まず最初のステップとして、最も未使用のスロットが多い列から1つのスロットを選択するとなっています。この場合、ACの列とBCの列にはそれぞれ6個の未使用スロットがあり、これはAB列の4つより多いので、（できるだけ左上から選ぶというルールに乗っ取って）AC列の一番上の”00”を選択します。そして、緑色にマークして右側の表（この表がテストケースに相当）に記入します。

続いて、未使用スロットの中で、そのうちの片方が右の表に出ているものを（AC列以外から）探します。たとえば、AB列の一番上である00は、右の表でAが0となっているので、これに該当します。同様にAB列の01もそうですし、BC列の00や10もこれに当てはまります。

さて、この時点で最も未選択スロットが多い行はBC行です（AB列の未選択スロットは4つ、BC列は6つ）。このため、BC列で、上の条件を満たすスロット（00と10）が次に選択する候補となります。PICTはこの中からランダムに選択するのですが、ここではその中で一番上のスロットである00を選択します（下の表でBC列の00が緑に、右の表ではＢ列が0に決定）。

これで1つのテストケースができました。この時点でABが00のスロットはこのテストケースでカバーされていますので、そのスロットも使用済みである緑にします。

続いて、最初と同様に最もカバーされていない列から1つのスロットを選択します。この場合、ACの列とBCの列がそれぞれ5個の未使用スロットがあって、これはAB列の3つより多いので、AC列の一番上にある01を選択します。

また、同様にBCから01を選んで、2つ目のテストケース“001”が出来上がります。

次も同様です。ACが02のスロットを選んで、さらにBCから02を選んでテストケースを作ると、こうなります。

ここで状況が変わります。この時点でABとACとBCどの列も未使用スロットは3つになりました。できるだけ左上から選ぶというルールに従うと、次に選択するスロットはAB列の01になります。

さて、ここでCの欄には何を入れたらよいでしょうか？　
AC列もBC列もそれぞれ残り3つのスロットがあります。しかし、AC列にはこれを満たす（Aが0）のスロットがありません。そこで、BC列でこれを満たす未選択スロットで、なおかつ一番上の10を選択することにします。

今度はACにほかの列より多い3つの未使用スロットがありますので、AC列から10を選択します。

そして、AB列から10を選択してこのテストケースを完成させます。

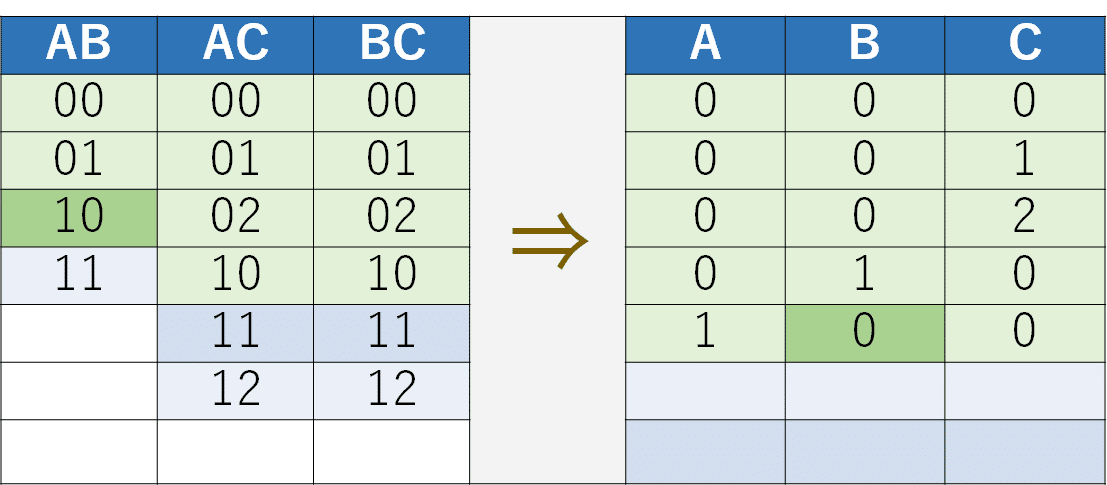
今度はAC列とBC列が残り2個で並んでいますので、AC列から11を選択します。

BC列が残り2スロットありますので、BC列から11を選択してB欄を埋めます。この際、AB列の11が満たされますので、同時にスロットを緑にします。

そして、AC列から12を選びます。残るBC列の12もうまく当てはまりますので、Bは自然と1に決まります。

これですべてのスロットが緑色になり、つまりすべての2因子間は網羅されたテストケースができたことになります。
テストケース数は7個で、全網羅した場合の12に比べて5つ減らせた、ということになります。下が最終的なテストケースです。

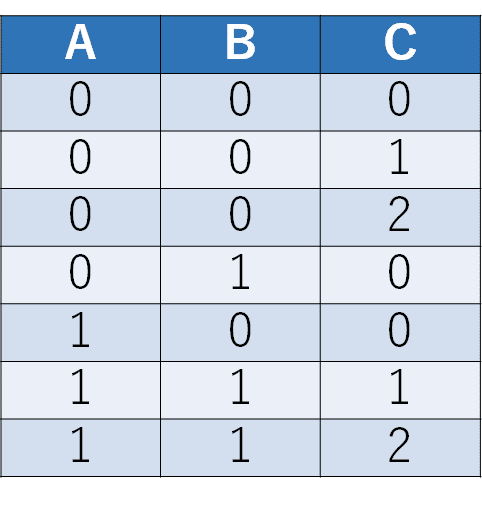
しかし、この表をよく見てみるといくつか気付くことがあります。例えばABが00のテストケースが3つもあります。また、ACやBCが00のテストケースが2つあったりして、意外と重複が多いなぁ、と感じられたかと思います。実はこのテストケースは、最適な（最小）なものではありません。

これに対して、例えば下のようなテストケースを考えてみましょう。このテストケースもすべての2因子間で全網羅を実現しつつ、テストケース数は6個と、上のテストケースより1つ少なくなっています。

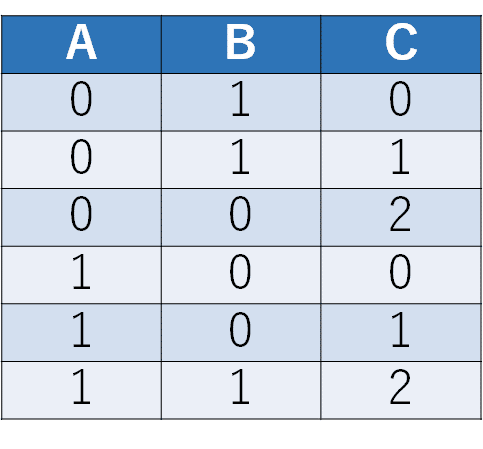
このテストケースでは、最初に選ぶスロットを左上にするというルールを守りつつ、2つ目の（主にBC列の）スロットを選ぶ際に、少し恣意的に良さそうなものを選んだことで、このように1つテストケースを減らすことができたのです。

こちらのテストケースの方がテストケースの数が少なくて良いのですが、PICTはテストケースを作れないのでしょうか？

実はここに貪欲法を使うことの問題が潜んでいるのです。貪欲法は、全体を見ないで局所的な最適化を行うことで実行時間を短縮するアルゴリズムですので、常に最適な答えを出すアルゴリズムではありません。そしてPICTはこの貪欲法と乱数で作られたツールなのですから、場合によっては（運が悪ければ）このように最適でないテストケースが生成される可能性があるのです。

実際このモデルをPICTで実行すると、ランダムシードとして0を与える（実行時のコマンドラインオプションに”/r:0”を指定する）と、テストケースは7個表示され、ランダムシード1を与える（”/r:1”）と6個のテストケースで網羅する最適なテストケースが生成ます。また、ランダムシードを0から99まで変えて実行して統計を取ってみたところ、87％の確率で6個のテストケースで網羅される結果が出ました（つまり今回の左上を選択するというのは残る13％のレアなケースでした）。

このような少ない因子と水準では、6個に対して7個と17％も多いテストケースが生成されてしまったわけですが、これが現実的な因子と水準の数では、多くの場合それほど大きさは生まれないと考えられます。試しに4因子で水準数がそれぞれ10、５、５、４、全網羅すると1000ケースになるモデルで、同様にランダムシードを0から99まで変えて100回試したところ、下のグラフのようになりました（横軸は生成されたテストケース数、縦軸はその回数）。

これを見ると、生成されたテストケース数は最小で51、最大で55と、その差は4つでした。いずれにせよ、全網羅時のテストケース数は1000なので、最悪の場合でも94.5％削減できており、十分効果はあると言えるでしょう。分散的にも中央値から±２と大きくないですし、また、およそ80％の確率でテストケース数が53以下になっていることも読み取れます。

なお、この（PICTの）論文でも“It can compute test suites that are comparable in size to other tools that exist in the field, and it is fast enough for all practical purposes.”と、書かれており、つまり他のツールと同程度のサイズのテストケース（のセット）を、十分素早く見つけ出せる、としています。もし運悪くテストケース数が多い結果がでてしまうことを避けたいなら、ランダムシードを変えながら10回ほど実行して、ケース数が最小のものを採用するような使い方をしてみるのもいいかもしれません。

おまけ

この論文は、アルゴリズムの解説以外に、PICTのリッチな機能についての説明や、今後の改良点なども書かれているのですが、ちょっと気になる記述にも出会いました。それが何かと言いますと、Pairwiseのテストケース作成は“NP完全分類される問題である”ことが証明されているというのです（Lei, Y., and K. C. Tai. “In-Parameter-Order: A Test-Generation Strategy for Pairwise Testing.” In Proceedings of the Third IEEE International High-Assurance Systems Engineering Symposium, pages 254–261, 1998.）。P、NP、NP完全、NP困難、これらはコンピューター用語の中でも“耳にしたことはあるけど理解できないもの”の代表（？）ですよね（私だけかもしれまえんが……）。NP完全がどういうものかについては、書くのは大変だし正しく書ける自信もないので、興味がある方はネットで調べていただければと思います。NP完全問題というと、充足性問題（SAT）や、ゲームの“ぷよぷよ”の連鎖数判定問題などもこれに含まれていたりします。そんなNP完全問題にPairwiseも分類される（つまり原理的にはPairwiseはぷよぷよの連鎖数判定問題に帰着できる？）というのも、ちょっとおもしろいな、と思いました。時間があったら（＋やる気があったら）この辺りも少し掘り下げてみたいなと思っています。

――――――――――――――――――――――――――――――――――

お問合せはお気軽に
https://service.shiftinc.jp/contact/

SHIFTについて（コーポレートサイト）
https://www.shiftinc.jp/

SHIFTのサービスについて（サービスサイト）
https://service.shiftinc.jp/

SHIFTの導入事例
https://service.shiftinc.jp/case/

お役立ち資料はこちら
https://service.shiftinc.jp/resources/

SHIFTの採用情報はこちら　　　
https://recruit.shiftinc.jp/career/