PICTのソースコードを読んでみる
こんにちは。株式会社SHIFT、自動化エンジニアの水谷です。
前回と前々回は、Pairwiseの考え方に従ってテストケースを作成してくれるツールの1つであるPICTについて書かれた論文を元に、PICTのアルゴリズムや機能について書きました。PICTはソースコードが公開されているので、今回はそのソースコードを読んで、どのように実装されているかを(ざっくりと)見てみたいと思います。
Githubからクローンする
PICTのソースコードはGithubで公開されていますので、誰でも簡単にクローンあるいはダウンロードして、Visual Studioを使ってビルドすることができます。PICTはC++で書かれているのですが、特殊なライブラリ等は使っていないため、C++に慣れている方であれば、読むことはできると思います。
なお、クローンするには、gitがインストールしてある必要がありますので、インストールされていない方はhttps://git-scm.com/からインストールしてください。
PICTのGithub URLは、こちらです。
https://github.com/microsoft/pict

「↓Code」と書かれたボタンをクリックすると、クローンするためのURLが表示され、またソースコードをZIP形式でダウンロードするためのボタンも表示されます。
クローンする場合はコマンドプロンプトから下ように「git clone」の後に、表示されたURLをコピペすればOKです。
git clone https://github.com/microsoft/pict.git下はC:\直下にクローンした様子です。

C:\pict 以下にソースコードがクローンされているはずです。
また、ソースコードをZIPファイルでダウンロードされた場合は、適当なフォルダに解凍してください。pict-masterというフォルダの中にソースコードが入っています。
PICTのソースコードには、Visual Studio 2017用のソリューションファイル「pict.sln」が入っていますので、Visual Studio 2017あるいは2019をお持ちの方はダブルクリックで開くことができます。
実行の流れ
PICTのソースコードの全部について書くとかなりの量になるので、組み合わせの生成にフォーカスして見ていきたいと思いますが、(コードを読まれる方の助けに多少はなるかと思いますので)その前にざっと実行の流れを簡単に見ていきましょう。
PICT.exeのmain関数は”pictcli”プロジェクトにある”pict.cpp”です。wmain関数はexecute関数を呼ぶだけのものであり、そのexecute関数はコマンドライン引数をパースして、モデルファイルを読み込む関数をコールし、その後GcdRunnerクラスのインスタンスを作成します。そして、このクラスのGenerateメソッドを呼びます。このメソッドは、組み合わせの生成を行うgenerateResultsメソッドを2回呼び出します。1回目は、異常系の水準を取り除いた状態で、正常系だけの組み合わせを生成し、2回目は異常系の組み合わせの作成です(異常系の水準が1つも含まれていない場合は前者のみが行われます)。
さて、そのgenerateResultsメソッドでは、まず階層化されたサブモデルに対して、組み合わせの生成を行い、その後全体の組み合わせの生成を行います。この組み合わせ生成はModelクラスのGenerateメソッドで行われ、この際生成方法として、MixedOrder、FlatOrder、Full、Flat、Randomに場合分けされます。通常の実行ではMixedOrderなので、generateMixedOrderメソッドへと飛びます。ここでは、各サブモデルでの組み合わせが取り込まれた後、核となるgcdメソッドが呼ばれます。
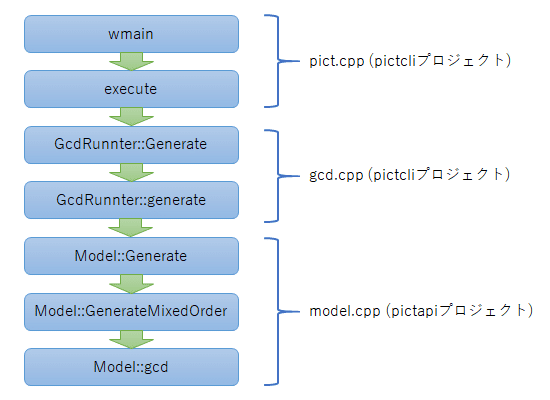
model::gcd メソッド
さてここからが本題です。model.cppにある、model::gcdメソッドについてみていきましょう(gcdは、generalized combinatorial designsの略です)。
このメソッドが行うことは、こちらの記事で書いたように、貪欲法を使って組み合わせを決めていくことで、論文には以下の疑似コードが掲載されています。

メソッドの引数であるvecComboの型はComboCollectionですが、これはCombinationクラスインスタンスのベクターです。Combinationは上の疑似コードにおける”combination”であり、ここに網羅すべきn因子間網羅の組み合わせがすべて入っています。
このメソッドで最初に行うのは、processExclusionsメソッドを呼んで、(モデルファイルにおいてIF文で記述したことで)取りえない組み合わせをリスト化しておきます。その他細かい処理があり、115行目からがメインループです。このループは未網羅のcombinationが無くなるまで繰り返されます。
いろいろなプロパティや変数を初期化するコードが続きますが、147行目からはSeeds(必ず現れることを要求している組み合わせ)に関するコードです。Seedsがリスト内に存在する場合は、先頭のものを取り出し、そのSeedに記載されているParameter(因子に相当するもの)をバインドしていきます(param->Bindをコール)。
// do we have unused seed data?
// if yes: bind those values, make sure combinations get marked, zero counts (including global) updated
if( !m_rowSeeds.empty() )
{
RowSeed &rowSeed = m_rowSeeds.front();
for( RowSeed::iterator ir = rowSeed.begin(); ir != rowSeed.end(); ++ir )
{
( ir->first )->MarkPending();
}
for( RowSeed::iterator ir = rowSeed.begin(); ir != rowSeed.end(); ++ir )
{
// find the parameter in the collection
Parameter* param = ir->first;
vector<Parameter*>::iterator found = find( m_parameters.begin(), m_parameters.end(), param );
assert( found != m_parameters.end() );
if( found != m_parameters.end() )
{
unbound -= param->Bind( ir->second, worklist );
}
}
m_rowSeeds.pop_front();
}このバインドが何をやっているのかなかなか理解しにくいのですが、そのパラメーターの値を確定するとともに、そのパラメーターが属するすべてのCombinationについて、バインドされていないParameter(因子)をworklistに追加しています(詳しくはBindメソッドの中身を参照してください)。
ここからは生成モードによって場合分けがあります。一般的なn因子間網羅のモードでは217行目からのelse内に進みます。
else内では、まだ未使用のパラメーターがある間(逆に言うと1つのテストケースが完成するまで)ループします。worklistが空(Seedがない場合、worklistは空の状態から始まる)の場合は、一番残りが多い因子の組み合わせから1つ水準の組(スロット)を見つけます。
int maxZeros = 0;
int maxMatch = 0;
int ties = 0;
int choice = -1;
for( int cidx = 0; cidx < static_cast<int>( vecCombo.size() ); ++cidx )
{
if( !vecCombo[ cidx ]->IsFullyBound() )
{
int open = 0;
int match = 0;
// Make sure there's a feasible value set
for( int vidx = 0; vidx < vecCombo[ cidx ]->GetRange(); ++vidx )
{
ComboStatus status = vecCombo[ cidx ]->Feasible( vidx );
if( Open == status )
{
++open;
}
else if( CoveredMatch == status )
{
++match;
}
}
// if combo has the most zeros
if( open > maxZeros )
{
choice = cidx;
ties = 1;
maxZeros = open;
}
// if number of zeros ties up with some previous choice, pick randomly
else if( open == maxZeros
&& maxZeros > 0
&& !( rand() % ++ties ) )
{
choice = cidx;
}
// no zeros were found anywhere yet, pick the best matching one
else if( maxZeros == 0
&& match > maxMatch )
{
choice = cidx;
ties = 1;
maxMatch = match;
}
// if there's a tie in match, pick randomly
else if( maxZeros == 0
&& match > 0
&& match == maxMatch
&& !( rand() % ++ties ) )
{
choice = cidx;
}
}
} // for cidxさて、どの列から因子間組み合わせから選択するかが決まりましたので、その中から候補となる(まだ網羅されていない)Combinationのリストを作ります。そしてそのリストからCombinationをランダムに1つ選択し、そのCombinationに入っている因子(Parameter)すべてをバインドしていきます。
// OK, we picked a combination, now pick a value set
vector<int> candidates;
for( int vidx = 0; vidx < vecCombo[ choice ]->GetRange(); ++vidx )
{
if( Open == vecCombo[ choice ]->Feasible( vidx ) )
{
candidates.push_back( vidx );
}
}
・・・
assert( !candidates.empty() );
int zeroVal = candidates[ rand() % candidates.size() ];
DOUT( L"Chose value " << zeroVal << L", unbound count was " << unbound << L".\n" );
// Bind the values corresponding to the zero
unbound -= vecCombo[ choice ]->Bind( zeroVal, worklist );
DOUT( L"After combo bind, unbound count was " << unbound << L".\n" );ここでバインドによって、(バインドされたパラメーターとペアになっているが未バインドなParameterが)worklistにパラメーターが蓄積されていますので、2回目のループは以下のコードが実行されます。
// worklist is NOT empty
else
{
// pull a parameter from the work list and pick a value
Parameter *param = worklist.GetItem();
assert( !param->GetBoundCount() );
DOUT( L"From worklist " );
param->Bind( param->PickValue(), worklist );
--unbound;
}worklistに値がある場合は、その1つが取り出され、PickValue()でえられる値がバインドされます。PickValueは、最もカバーされていないCombinationを返すメソッドですが、ここが貪欲法の要の部分になります。しかし、重みづけなども考慮してスロットを選択するので、やや複雑です。
//
// This method chooses the value for this parameter in the current context
//
int Parameter::PickValue()
{
assert(!m_bound);
int maxComplete = 0;
int maxTotal = 0;
int bestValue = 0;
int bestValueCount = 0;
m_bound = true; // a white lie to facilitate Combination::Feasible()
for (int value = 0; value < m_valueCount; ++value)
{
int totalZeros = 0;
int complete = 0;
// try binding that value and see how feasible it is
m_currentValue = value;
for (ComboCollection::iterator iter = m_combinations.begin(); iter != m_combinations.end(); ++iter)
{
int zeros = (*iter)->Feasible();
totalZeros += zeros;
if ((*iter)->GetBoundCount() >= (*iter)->GetParameterCount() - 1)
{
if (zeros)
++complete;
if ((*iter)->ViolatesExclusion())
{
// make sure we don't pick this value, and move on
totalZeros = -1;
complete = -1;
break;
}
}
}
if (complete > maxComplete)
{
maxComplete = complete;
bestValue = value;
maxTotal = totalZeros;
bestValueCount = 1;
}
else if (complete == maxComplete)
{
if (totalZeros > maxTotal)
{
bestValue = value;
maxTotal = totalZeros;
bestValueCount = 1;
}
else if (!m_valueWeights.empty() && 0 == totalZeros && 0 == maxTotal)
{
// Arbitrary choice - we already have this parameter covered
// Use weights if they exist
bestValueCount += GetWeight(value);
if (rand() % bestValueCount < GetWeight(value))
{
bestValue = value;
}
}
else if (totalZeros == maxTotal && !(rand() % ++bestValueCount))
{
bestValue = value;
maxTotal = totalZeros;
}
}
}
m_bound = false;
// What if bestValueCount is 0 here due to exclusions?
// That would be a bug, but better put in a check.
if( m_task->GetGenerationMode() != Preview )
{
assert( bestValueCount > 0 );
if( bestValueCount <= 0 )
{
throw GenerationError( __FILE__, __LINE__, GenerationFailure );
}
}
return bestValue;
}ざっと動作内容を書くと、そのParameter(因子)がとりうるすべての値に対して、それが属するCombinationで使われていないものの数を数えます(それがcomplete)。そして、それが一番大きなものを選ぶのですが、同数のものがあった場合は、このParameterが属するCombinationないでバインドされていないParameterの数が多いほうを選択します。それでも同じ場合はWeightを考慮して選択します。なお、Weightがない場合はランダムで選ぶことになります。
Parameterが決まったら、これをバインドして、worklistが無くなるまでこれを繰り返します。worklistが空になれば、また一番残りが多い因子の組み合わせから1つのCombinationを選ぶ、という作業に戻ります。これを繰り返すことで1つのテストケースができていきます。その後は、カバーされていないCombinationがあれば、次のテストケースを同じ要領で作っていき、カバーされていないCombinationが無くなれば終了です。
軽い気持ちで「あの疑似コードがどう実装されているのかな?」と、コードを見始めたのですが、やはり、2因子網羅ではなく一般化したn因子網羅であることや、たくさんの機能を盛り込んでいることもあり、思ったより複雑だなと思いましたが、いかがでしょうか?
ちなみに、週末の半日くらいコードに向かっていれば理解できるかなと思っていましたが、ちょっと甘かったです。。。しっかり読み込めてないので、まだ理解できていない部分もありますし、PickValueはほんとにこれが最適なコードなのかな? という疑問も出てきたりしましたが、個人的には最近あまりアルゴリズムが面白いツールのコードを読む機会がなかったこともあり、コードを読むこと自体が楽しめました。C++の良い教材になりそうなコードですし、もし興味持たれた方がいらっしゃいましたら是非読み込んでみてください。
――――――――――――――――――――――――――――――――――
執筆者プロフィール:水谷 裕一
大手外資系IT企業で15年間テストエンジニアとして、多数のプロジェクトでテストの自動化作業を経験。その後画像処理系ベンチャーを経てSHIFTに入社。
SHIFTでは、テストの自動化案件を2件こなした後、株式会社リアルグローブ・オートメーティッド(RGA)にPMとして出向中。RGAでは主にAnsibleに関する案件をプレーイングマネジャーとして担当している。
お問合せはお気軽に
SHIFTについて(コーポレートサイト)
https://www.shiftinc.jp/
SHIFTのサービスについて(サービスサイト)
https://service.shiftinc.jp/
SHIFTの導入事例
https://service.shiftinc.jp/case/
お役立ち資料はこちら
https://service.shiftinc.jp/resources/
SHIFTの採用情報はこちら
https://recruit.shiftinc.jp/career/

